チューリング完全あくあたん

Sorry, this entry is only available in 日本語.

この記事はあくあたん工房 Advent Calendar 2021の15日目です．

チューリング完全とは？

ある計算システムがチューリング完全であるとは，万能チューリングマシンと同じ計算能力を持つことを指します．万能チューリングマシンはチューリングマシンを模倣できるチューリングマシンであり，現在のどんな計算機が解ける問題でも解くことができると考えられています．

あるシステムがチューリング完全かを判定するのは難しい問題になるため，チューリング完全であることがすでに判明しているシステムの模倣ができる場合，そのシステムもチューリング完全であると言えます．

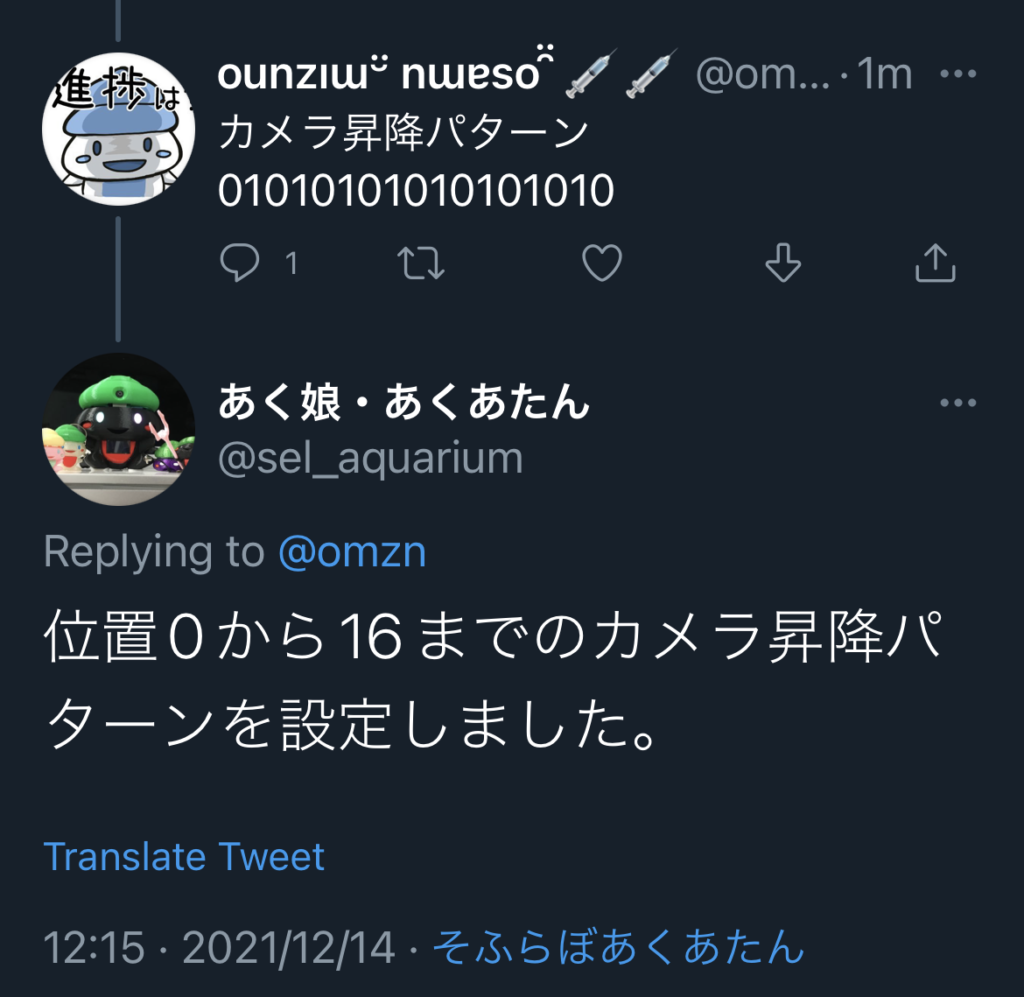
水槽カメラ昇降パターン

あくあたん義体はレールの上のマーカー(位置)を読み取って水平方向に進むことができます．また，レールの位置上でカメラの垂直方向を昇降させることができます．レールの位置はあくあたんbotからの指令により移動させることが多いですが，カメラの昇降については指令を飛ばすことが少なくなっています．そこで，カメラの昇降については，ランダムに近いけれども特定のルールを利用した動作をさせたいと思います．

レールの位置には1ビットの情報が付与できるものとします．あくあたんは位置上でカメラ垂直方向を上下させることができますので，ここではある位置において，カメラを1段上昇させるなら1，1段下降させるなら0とします．この情報をカメラ昇降パターンと呼びます．あくあたんはこの情報を使って，その位置を踏んだときにカメラ垂直位置を変更します．

各位置での昇降動作を初期状態としてあくあたんに教えることができます．

水槽カメラ昇降パターン更新規則

さて，このままではいつも同じ位置で上下するだけで面白くありません．
そこで，あくあたんが水槽の一番左か右(位置0か16)に到達した時点で，カメラを昇降させるパターンを変更したいと思います．

このパターンの変更は，各位置において，左右両隣の位置の状態に応じて変更するようにします．そうすると，次のような遷移表を書くことができます．3ビットの真ん中が当該位置であり，左右と自分自身の値に応じて，自分自身の変更後の値が決まります．

変更前(左，自身，右)	変更後
0, 0, 0	x, 1, x
0, 0, 1	x, 0, x
0, 1, 0	x, 1, x
0, 1, 1	x, 0, x
1, 0, 0	x, 1, x
1, 0, 1	x, 0, x
1, 1, 0	x, 1, x
1, 1, 1	x, 0, x

これを「カメラ昇降パターン更新規則（更新規則）」と呼びます．

例えば，上記更新規則では，ある時点のカメラ昇降パターンが「0001111000111100」であった場合，次のように更新されます．なお，実装の都合上，右端と左端はつながっており，ループしているものとします．

0 0 0 1 1 1 1 0 0 0 1 1 1 1 0 0
↓
1 1 0 0 0 0 1 1 1 0 0 0 0 1 1 1

更新規則は変更後のビットが取る値の並び8つで識別できます．上記の規則では01010101となります．すなわち 2^8 = 256個の更新規則のいずれかを採用することになります．この更新規則はビットの並びを2進数として読んだ値を10進表現した数字で表されます．例えば，上の表の更新規則は 01010101 ですから64+16+4+1 = 85で，更新規則85と呼びます．あくあたんにはこの更新規則番号を伝えれば，その更新規則を採用することになります．

あくあたんが一番左か一番右の位置へ移動すると，このカメラ昇降パターン更新規則が適用され，各位置でのカメラ昇降パターンが更新されることになります．

まとめると，あくあたん義体には「カメラ昇降パターンの初期状態」「カメラ昇降パターンの更新規則」を設定することができ，自律制御時のカメラ位置はこれに従って昇降させることになります．またあくあたん義体のレール上の移動に伴い，カメラ昇降パターンは次世代へと更新されることになります．

セル・オートマトン

ここまでで説明してきたカメラ昇降パターンを変化させる動作は，実は1次元セル・オートマトンと呼ばれるものと同じです．1次元セル・オートマトンは無限の1次元セルのビットパターンを更新規則によって変更し，世代を重ねていきます．2次元のセル・オートマトンの例としてはライフゲームなどがよく知られていますね．

1次元セル・オートマトンの256種類の規則は，どのような状態になるかで4つのクラスに分類されます．

クラス1: 最終的に全体が均質な状態に遷移するもの(規則248)など)
クラス2: 最終的に局所的なパターンを繰り返したり，安定状態になるもの(規則123)など)
クラス3: カオス的なパターンを示すもの(規則30)など)
クラス4: カオス的なパターンと規則的パターンが共存する(規則110)など)

クラス3に属する規則90は，1ビットのみが1の初期状態からフラクタル図形を生成することが知られています．クラス4は複雑な計算状態を内包することを表しています．そして，クラス4に分類される「規則110」はチューリング完全であることが証明されています．

規則110の遷移

変更前(左，自身，右)	変更後
0, 0, 0	x, 0, x
0, 0, 1	x, 1, x
0, 1, 0	x, 1, x
0, 1, 1	x, 1, x
1, 0, 0	x, 0, x
1, 0, 1	x, 1, x
1, 1, 0	x, 1, x
1, 1, 1	x, 0, x